23徐聖庭 夢千大師與龜兔賽跑

今天又有講座啦啦啦啦啦=]段考後雖然不太想早起，但去年的講座給我很大的印象=]
似乎只有我記得他們去年來過耶......在仁愛樓4樓那次.....懵懂的7年級XDD
去年的講座主題是邏輯思考，正好是我最愛的推理，所以這次我充滿期待~~~~結果呢!!!!
竟然是數列阿= =   好遙遠的感覺.....南山高中那時的亞太奧林匹亞集訓?(這人在幹麻阿)
等比等差階層希格瑪C幾取幾......(瘋了阿
這不是高一的課程嗎= =記憶好像還沒隔很遠阿(大誤)
所以呢，我又開始回味那一團一團的數字XDD
其實呢~~我們還沒學數學時，就開始先學數列了!!!怎麼說呢?
誰不是從1.2.3.4.5.6.7.8.9.10開始學的?   (我!!!!我先學0  (打飛
這是一個首項=1，公差=1的等差數列!!!!!
還有學乘法時，當然就學到等比數列啦!!!
就這麼單純!!數列就被我們輕鬆學會了，那為啥看起來這麼的艱深難懂呢?
奇奇怪怪的符號，只是為了表達出這數列的規律、要取哪幾項、和或積是多少......等等，
只要了解就很好上手啦!!!!排列組合還有個重頭戲叫[[[[交集與聯集]]]]]]，
關鍵字就是[且]還有[或]，舉個例子，
有好多的英文單字、由字母組成，有包含F的就叫[F集合]，
有包含CK的就叫[CK集合]，當我們要找有F[或]有CK的字時，就是要找[F聯集CK]，
寫出來的符號我打不出來，有興趣自己去找一下(燦笑)
(別無他意，只是舉個比較簡單的例子)

回到數列，最有名的當然是[斐波那契]數列，又譯[費波那西]數列
符號就是F(x)，但是有兩種說法，一種包含第零項，一種是直接從第一項開始。
請別無聊的學某凱捷同學說什麼廢物垃ㄌㄚ圾ㄐㄧ數列，這是一種侮辱!!
F₀ = 0，F₁ = 1，F_n = F_{n - 1} + F_{n - 2}，n≧3，
即為0.1.1.2.3.5.8.13.......依此類推，然後又可以扯上鼎鼎大名的黃金分割比，
相鄰兩項比值會趨近於1.618!!!!!!當然，前幾項看不出來= =
(阿勒，我講不完了)
這數列就先跳過跳過，咱們回到一開始的魔術~~~~會很神奇嗎?
這級數總和=第七項乘11，把第一項代M第二項代N去求一求，
慢慢的解阿，就發現很神奇的事情!!!(打飛)這我要重說嗎......
這還不怎重要，我閒閒沒事找到了另一個無聊的規律並加以證明了~~~
從第一項加到第K項和會等於第K減2項，這是用代數代的呦~~~
老師也說了[很好，很厲害呢!!!!我幫你去要禮物!!!]
結果拿到一個便條卡的小冊子(冏)反正我也不期望會有什麼東東= =
不過我有說謝謝老師歐!!!!我還是看起來很有禮貌的!!!!!

然後下節課咩~~~一直搶答搶的好累~~~龜兔賽跑進先到????(好故意呢XD
(我還要再打一大串?饒了我吧~~~~(睏~~
龜兔賽跑就是求數列的極限，這也扯到了數列的收斂，
一個數列{a_n}，使得，
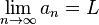其中L為一確定的常數，亦即數列{a_n}隨著n的增加而趨近於L。
 所以理論上他們間的距離會越來越短，但始終距離會大於零。
不過警察就是不會追不到小偷，狗不會咬不到自己的尾巴(誤)?
等比級數的公比若小於1，和就會趨近於1，還有幾何圖形的例子，
讓這收斂簡單了許多，也讓我的王子麵大增~(杜修也好多呢~)
最後就是連線遊戲，因為獎品沒有像去年的可樂果+百事可樂，
我們這組好懶散呢~(社會是現實的!!)
我們當然不想因為獎品造成幼幼班的分裂XDDD(好個冠冕堂皇)
然後講座就結束啦~~~~(累)
還是很開心啦=]感謝各位老師們!!!!!
雖然沒有讓我更了解數列，但還是有讓我學到好久不見的數列!!!!
(會不會看我報告看到煩阿?這是網誌嗎XDDD)
                                                                                               END
                                                                                                                    823 徐聖庭